Paquetes

  • numpy
import numpy as np

from df.number_internals import show_float
from df.array_internals import show_array_details

Recordando la semana pasada, los arreglos:

  • Tienen un tamaño pre-determinado
  • Tienen que ser "rectangulares"
  • Todos los elementos tienen el mismo tipo
  • Los elementos son números

A partir de este punto, vamos a conocer sobre:

  • Representación de arreglos en memoria
  • Representación de números en memoria

Arreglos en memoria

Los arreglos en NumPy implementados de forma compacta en memoria; la información numérica está almacenada de forma contigua (un número despues del otro) con un pequeño encabezado que describe cómo es que el arreglo debe ser manipulado.

No importa si estamos hablando de un arreglo unidimensional o de un tensor de 6 dimensiones, los arreglos en NumPy son planos, un número después del otro con un poco de información extra al inicio:

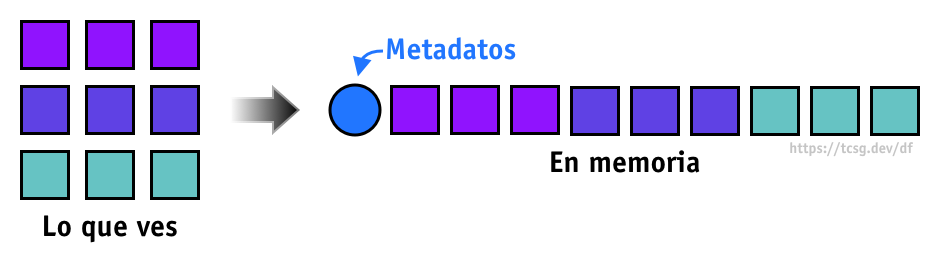
Zancadas o strides

El truco detrás de la implementación de los arreglos es el uso de algo llamado zancada (!???!) o stride en inglés. Estas strides especifican cómo es que se debe indexar el arreglo. Hay un stride por cada dimensión.

Se llama zancada porque se usa para especificar qué tan grande es el "paso" en bytes que se debe dar para acceder a cada uno de los elementos; y este es el truco que le permite a NumPy mantener el arreglo como una sola secuencia plana de números:

Es más claro cuando vemos este concepto aplicado a un arreglo de dos dimensiones, para calcular la ubicación en memoria de el elemento en la posición [\(i\), \(j\)] se puede usar la fórmula:

\(location = i * stride_0 + j * stride_1\)

Podemos generalizar esta idea para arreglos de 3, 4 y demás dimensiones.

Transformaciones rígidas

base = np.zeros((3, 4), dtype=np.float32)
show_array_details(base)

Shape:      (3, 4)
Stride:     (16, 4)
Type:       float32
Elements:   12
Bytes:      48
Bits:       32

print("Original")
show_array_details(base)

Original
Shape:      (3, 4)
Stride:     (16, 4)
Type:       float32
Elements:   12
Bytes:      48
Bits:       32

print("Transpuesta")
base_t = base.T
show_array_details(base_t)

Transpuesta
Shape:      (4, 3)
Stride:     (4, 16)
Type:       float32
Elements:   12
Bytes:      48
Bits:       32

flipud = np.flipud(base)
print("Invertida")
show_array_details(flipud)

Invertida
Shape:      (3, 4)
Stride:     (-16, 4)
Type:       float32
Elements:   12
Bytes:      48
Bits:       32

print("Reflejada")
fliplr = np.fliplr(base)
show_array_details(fliplr)

Reflejada
Shape:      (3, 4)
Stride:     (16, -4)
Type:       float32
Elements:   12
Bytes:      48
Bits:       32

rotated = np.rot90(base)
print("Girada 90 grados")
show_array_details(rotated)

Girada 90 grados
Shape:      (4, 3)
Stride:     (-4, 16)
Type:       float32
Elements:   12
Bytes:      48
Bits:       32

Tipos de datos en NumPy

Por default habrás visto más arriba, los tipos de dato de NumPy son float64 si creamos arreglos con números flotantes e int32 si estamos creando arreglos con números enteros, pero no son los únicos

Tipos numéricos

Enteros

Los enteros representan números sin partes fraccionales; hay de dos tipos: con signo y si signo. La representación de ellos es en forma de una cadena binaria.

Aquí una tabla con los detalles sobre algunos de estos números:

Nombre bytes Mínimo Máximo
int8 1 -128 127
uint8 1 0 255
int16 2 -32,768 32,767
uint16 2 0 65,535
int32 4 -2,147,483,648 2,147,483,647
uint32 4 0 4,294,967,295
int64 8 -9,223,372,036,854,775,808 +9,223,372,036,854,775,807
uint64 8 0 18,446,744,073,709,551,615
Desbordamiento

Si una operación se sale de los límites del número entero del tipo de dato ocurre un desbordamiento o overflow. En muchos sistemas el número simplemente va a reinciar desde el valor más pequeño:

int_array = np.array([100, 110, 120], dtype=np.int8)
print(int_array)
print(int_array + 20)

[100 110 120]
[ 120 -126 -116]

uint_array = np.array([100, 110, 120], dtype=np.uint8)
print(uint_array)

print(uint_array + 20)
print(uint_array + 150)

[100 110 120]
[120 130 140]
[250   4  14]

Floats

IEEE 754

La forma más común de representar números de punto flotante es el estandar IEEE 754, que especifica una forma de representar números y representaciones específicas para representar números "especiales".

Este es un resumen de los tipos definidos:

Name Nombre común Base Mantissa Bits del exponente Sesgo exponente \(E_{min}\) \(E_{max}\)
binary16 Precisión media 2 11 5 2^4−1 = 15 −14 +15
binary32 Precisión simple 2 24 8 2^7−1 = 127 −126 +127
binary64 Precisión doble 2 53 11 2^10−1 = 1023 −1022 +1023
binary128 Precisión cuádruple 2 113 15 2^14−1 = 16383 −16382 +16383
binary256 Precision óctuple 2 237 19 2^18−1 = 262143 −262142 +262143

Simples y dobles

Remarcadas en la tabla de arriba están las precisiones simple y dobles, puesto que estas son las más comunes en la actualidad. Como te podrás imaginar, float32 ocupa 32 bits (4 bytes) por número y float64 usa 64 bits (8 bytes) por número.

Inclusive las GPUs de la actualidad siguen usando float32 por default, algunas llegan a float64, pero la verdadera rapidez proviene de usar el número de 32 bits.

Sistemas de precisiones fuera de 32 y 64 bits son raras y muy limitadas; en particular, 128 y 256 son usadas cuando se habla de aplicaciones de escala astronómica:

In addition, the range from the Sun to the pulsar source may exceed ten thousand light years away, so it needs at least quadruple precision (128 bits of floating point representation). Otherwise, the numerical error of computing will result in poor navigation accuracy.In addition, the range from the Sun to the pulsar source may exceed ten thousand light years away, so it needs at least quadruple precision (128 bits of floating point representation). Otherwise, the numerical error of computing will result in poor navigation accuracy. ~ Autonomous Navigation of Mars Probes by Single X-ray Pulsar Measurement and Optical Data of Viewing Martian Moons

🚨 NumPy no soporta números de 128 a 256

Representación binaria

Un float se representa binariamente por tres partes, cada una de estas partes es... un entero 🤪. Cada una de estas partes tiene un nombre específico:

  • Signo
  • Mantissa
  • Exponente

Para reconstruir un número flotante a partir de estos tres números debemos seguir la siguiente fórmula:

\(signo \times (1 + mantissa) \times 2^{exponente}\)

Flotantes

show_float(1.0)

Sign | Exp         | Mantissa
   0 | 01111111111 | 0000000000000000000000000000000000000000000000000000
   1 |           0 |                                                  0.0
  = 1 * 1.0 * 2^0
  = 1 * 1.0 * 1
  = 1.00000000000000000000

show_float(-1.0)

Sign | Exp         | Mantissa
   1 | 01111111111 | 0000000000000000000000000000000000000000000000000000
  -1 |           0 |                                                  0.0
  = -1 * 1.0 * 2^0
  = -1 * 1.0 * 1
  = -1.00000000000000000000

show_float(4.0)

Sign | Exp         | Mantissa
   0 | 10000000001 | 0000000000000000000000000000000000000000000000000000
   1 |           2 |                                                  0.0
  = 1 * 1.0 * 2^2
  = 1 * 1.0 * 4
  = 4.00000000000000000000

show_float(1e-8)

Sign | Exp         | Mantissa
   0 | 01111100100 | 0101011110011000111011100010001100001000110000111010
   1 |         -27 |                                  0.34217728000000003
  = 1 * 1.34217728 * 2^-27
  = 1 * 1.34217728 * 7.450580596923828e-09
  = 0.00000001000000000000

show_float(1.5e200, type_=np.float32)

Sign | Exp      | Mantissa
   0 | 11111111 | 00000000000000000000000
   1 |      128 |                     0.0
Infinite/NaN

Enteros

Recordemos que para float64 el tamaño de la mantissa es de 53 bits, lo cual significa que cualquier entero en los rangos \(-2^{53}\) to \(2^{53}\) es representable. Números fuera de este rango no son representados exactamente.

entero = 2 ** 53 - 1
show_float(1.0 * entero)
print(entero)

Sign | Exp         | Mantissa
   0 | 10000110011 | 1111111111111111111111111111111111111111111111111111
   1 |          52 |                                   0.9999999999999998
  = 1 * 1.9999999999999998 * 2^52
  = 1 * 1.9999999999999998 * 4503599627370496
  = 9007199254740991.00000000000000000000

9007199254740991

entero = 2 ** 53 + 1
show_float(1.0 * entero)
print(entero)

Sign | Exp         | Mantissa
   0 | 10000110100 | 0000000000000000000000000000000000000000000000000000
   1 |          53 |                                                  0.0
  = 1 * 1.0 * 2^53
  = 1 * 1.0 * 9007199254740992
  = 9007199254740992.00000000000000000000

9007199254740993

entero = 3 ** 55
show_float(1.0 * entero)
print(entero)

Sign | Exp         | Mantissa
   0 | 10001010110 | 0010000010011010000111010101101101000000000111001100
   1 |          87 |                                  0.12735160329622186
  = 1 * 1.1273516032962219 * 2^87
  = 1 * 1.1273516032962219 * 154742504910672534362390528
  = 174449211009120166087753728.00000000000000000000

174449211009120179071170507

Errores

Cuando operamos con números flotantes podemos provocar errores a nivel de hardware:

  • Operación inválida: cuando provocamos una operación sin un valor definido: \(\frac{0}{0}\), \(\sqrt{-1}\)
  • División entre cero: ...
  • Underflow: cuando el resultado de una operación es más pequeño que el número más pequeño que se puede representar (usualmente el resultado se redondea a cero)
  • Overflow: cuando el resultado de una operación es más grande que el número más grande que se puede representar.
  • Resultado inexacto: cuando una operación va a generar un resultado inexacto por redondeo

Las excepciones son generadas en el hardware y son escaladas por el sistema operativo y pueden o no ser interceptadas por alguna capa antes de llegar al usuario. Cada sistema (o framework) puede decidir qué hacer con ellas: informar al usuario, detener la ejecución del programa...

NumPy por default intercepta los errores y le informa al usuario a través de un warning:

np.array(0.0) / np.array(0.0)

<ipython-input-1-93b8fe404e2e>:1: RuntimeWarning: invalid value encountered in true_divide
  np.array(0.0) / np.array(0.0)





nan

np.array(1.0) / np.array(0.0)

<ipython-input-1-f123338f04e5>:1: RuntimeWarning: divide by zero encountered in true_divide
  np.array(1.0) / np.array(0.0)





inf

np.array(0.1) * np.array(1e-307)

1e-308

np.array(2.0) / np.array(3.0)

0.6666666666666666

Números especiales

¿Cero negativo?

Gracias a la forma en que se pueden representar los números bajo el estándar IEEE 754, podemos tener dos ceros.

show_float(-0.0)

Sign | Exp         | Mantissa
   1 | 00000000000 | 0000000000000000000000000000000000000000000000000000
  -1 |       -1023 |                                                  0.0
  = -1 * 1.0 * 2^-1023
  = -1 * 1.0 * 1.1125369292536007e-308
  = -0.00000000000000000000

show_float(0.0)

Sign | Exp         | Mantissa
   0 | 00000000000 | 0000000000000000000000000000000000000000000000000000
   1 |       -1023 |                                                  0.0
  = 1 * 1.0 * 2^-1023
  = 1 * 1.0 * 1.1125369292536007e-308
  = 0.00000000000000000000

Dos infinitos

También existe una definición explícita para infinito

show_float(np.inf)

Sign | Exp         | Mantissa
   0 | 11111111111 | 0000000000000000000000000000000000000000000000000000
   1 |        1024 |                                                  0.0
Infinite/NaN

show_float(-np.inf)

Sign | Exp         | Mantissa
   1 | 11111111111 | 0000000000000000000000000000000000000000000000000000
  -1 |        1024 |                                                  0.0
Infinite/NaN

0 * np.inf

nan

No es un número - NaN (Not A Number)

Otro número muy especial, usado para representar valores inválidos:

  • \(\frac{0}{0}\)
  • \(\frac{\infty}{\infty}\)
  • \(\infty - \infty\) o \(-\infty + \infty\)
  • \(0 \times \infty\)
  • \(\sqrt(x)\) para toda \(x < 0\)
show_float(-np.nan)

Sign | Exp         | Mantissa
   1 | 11111111111 | 1000000000000000000000000000000000000000000000000000
  -1 |        1024 |                                                  0.5
Infinite/NaN

🚨 NaN se propaga, una vez que en un cálculo se genera un NaN, cualquier operación en la que este se vea involucrado resultará en NaN

np.nan * np.inf

nan

Redondeo y precisión

Debido a las limitaciones en tamaño de bits para representar ciertos números los flotantes son propensos a presentar errores de redondeo:

show_float(1.0 + 1e-2)

Sign | Exp         | Mantissa
   0 | 01111111111 | 0000001010001111010111000010100011110101110000101001
   1 |           0 |                                 0.010000000000000009
  = 1 * 1.01 * 2^0
  = 1 * 1.01 * 1
  = 1.01000000000000000888

show_float(1.0 + 1e-4)

Sign | Exp         | Mantissa
   0 | 01111111111 | 0000000000000110100011011011100010111010110001110001
   1 |           0 |                                9.999999999998899e-05
  = 1 * 1.0001 * 2^0
  = 1 * 1.0001 * 1
  = 1.00009999999999998899

show_float(1.0 + 1e-8)

Sign | Exp         | Mantissa
   0 | 01111111111 | 0000000000000000000000000010101011110011000111011100
   1 |           0 |                                 9.99999993922529e-09
  = 1 * 1.00000001 * 2^0
  = 1 * 1.00000001 * 1
  = 1.00000000999999993923

show_float(1.0 + 1e-16, type_=np.float128)

Sign | Exp             | Mantissa
   0 | 000000000000000 | 0111111111010101100001001100110000111111111111111000000000000000000000000000000000000000000000000000000000000000
   1 |          -16383 |                                                                                              0.49935178743908004
  = 1 * 1.49935178743908 * 2^-16383
  = 1 * 1.49935178743908 * 0.0
  = 1.00000000000000000000

🚨 NUNCA uses números flotantes para cálculos financieros; un error gracias al redondeo (por más pequeño que sea) repetido muchas veces puede resultar en un error gigantezco. Python tiene un módulo llamado decimal que es lento, pero seguro.

Algunas reglas...

El redondeo en números flotantes es un problema que para la mayoría de aplicaciones no es tan grande; aún así existen algunas cosas que podemos hacer para mitigarlo a la hora de escribir código:

  • Error de magnitud: evita sumas \(x + y\) donde \(x\) e \(y\) sean de magnitudes diferentes.
  • Error de magnificación: evita divisiones \(\frac{x}{y}\) en donde \(y\) sea muy pequeña.
  • Error de cancelación: evita restas \(x - y\) en donde \(x \simeq y\)
(1e30 + 1.0) - 1e30

0.0

(1e30 - 1e30) + 1.0

1.0

Comparaciones numéricas

Gracias a estos errores de redondeo, comparaciones directas entre números flotantes pueden resultar "incorrectas", y por tanto no es apropiado usarlas:

x = 0.1
y = 50000.0
z = 0.1
x = (x + y) - y

print(x == z)
print(x - z)

False
-1.4551970739518083e-12

La solución es usar la diferencia absoluta comparada contra un determinado valor muy pequeño:

\(|x-z|<\epsilon\)

x = 0.1
y = 50000.0
z = 0.1

epsilon = 1e-8

x = (x + y) - y

print(abs(x - z) < epsilon)

True

All close

NumPy al rescate con la función: np.allclose:

x = 0.1
y = 50000.0
z = 0.1

x = (x + y) - y

print(x, z)
np.allclose(x, z)

0.09999999999854481 0.1





True

x = np.full((3, 3), 0.1)
y = np.full((3, 3), 500000000.0)
z = np.full((3, 3), 0.1)

x = (x + y) - y


print(x)
print(z)
np.allclose(x, z)

[[0.10000002 0.10000002 0.10000002]
 [0.10000002 0.10000002 0.10000002]
 [0.10000002 0.10000002 0.10000002]]
[[0.1 0.1 0.1]
 [0.1 0.1 0.1]
 [0.1 0.1 0.1]]





True

Referencias

Libros

  • Elegant SciPy: The Art of Scientific Python: México · España · US
  • High Performance Python: Practical Performant Programming for Humans: México · España · US

Sitios web