Notación O grande
La O mayúscula es una notación matemática también conocida Bachmann–Landau notation, asymptotic notation, notación o grande. Y esta nos ayuda a describir el comportamiento de una función "al límite". Esta notación tiene muchos usos en realidad, sin embargo el que nos interesa ahora es el que se le da en las ciencias de la computación.
En las ciencias de la computación esta notación nos ayuda a dscribir el comportamiento de un algoritmo, ya sea temporal (cuantas unidades de tiempo va a tardar en ejecutarse) o en espacio (cuanta memoria va a ocupar mientras se ejecuta), esto basado en la cantidad de entradas que recibe y sobre los que opera. A este "comportamiento" también se le conoce como complejidad de un algoritmo. Este análisis de complejidad nos sirve generalmente cuando las entradas de el algoritmo analizado son muy grandes.
Por poner un ejemplo, supón que tu amiga te va a dar un regalo, pero para hacer las cosas más interesantes tomó N cajas, las colocó en una fila y escondió el regalo en una de ellas. Entonces tu tienes que ir destapando cada caja hasta encontrar tu regalo, sabes que tendrás que abrir a lo mucho N cajas, entonces podríamos decir que tu "algoritmo" de búsqueda tiene una complejidad temporal de O(n).
Algo bastante útil de este análisis es que funciona independientemente de quién o en donde se ejecute el algoritmo, siguiendo con el ejemplo de las cajas y el regalo. Puede que tu te tardes 3 segundos en abrir cada caja, pero tu amiga las pueda abrir en 2. No importa cual tarde menos, si los dos usan el mismo algoritmo, la complejidad será la misma, O(n).
De igual manera si determinado algoritmo se tarda veinte segundos en mi computadora pero en los servidores de Google se tarda 2, se podría establecer la unidad de tiempo en dos segundos y decir que "en mi computadora se tarda C unidades de tiempo" en donde C es una constante que dependerá únicamente de las características del entorno en donde se ejecuta, no del algoritmo que está siendo ejecutado.
Una forma bastante rápida y generalmente útil para poder calcular la complejidad de un algoritmo es fijarse en el tipo de operaciones que realiza, por ejemplo si se trata de un cálculo matemático, como el cálculo de las soluciones de una ecuación de segundo grado, se dice que tiene una complejidad constante O(1), ya que no importa que tan grandes sean los coeficientes de entrada, siempre realizará la misma cantidad de operaciones para llegar al resultado.
Por otro lado, si tu algoritmo requiere recorrer un arreglo unidimensional de N elementos (como el ejemplo de las cajas), sabes que cuando menos se va a tardar N unidades de tiempo en ejecutarse, osea O(n), así mismo si tienes que recorrer una matriz de NxN se tardará N^2 y así sucesivamente.
Entre las complejidades mas comunes también está la de O(n log n), que presentan algunos algoritmos que van dividiendo o descartando parte de las entradas sobre las que opera, como el Quicksort o la búsqueda binaria.
También existe una complejidad con la que debes tener mucho, pero mucho cuidado y esta es la complejidad O(n!), ya que con tan solo una entrada de 10 elementos el algoritmo estaría haciendo 3628800 operaciones. Un ejemplo de este problema es el del agente viajero:
Imagina que quieres visitar las capitales de todos los países de la Unión Europea, pero quieres encontrar la manera más corta para hacerlo entonces te pones a calcular todas las posibilidades que tienes… ¡mala idea! hay 3.0488834e+29 posibilidades para calcular, es entonces cuando surgen otro tipo de algoritmos que son un poco más complejos de analizar.
Aquí solamente hablé de algunas de las complejidades más comunes, pero también existen otras muy usadas:
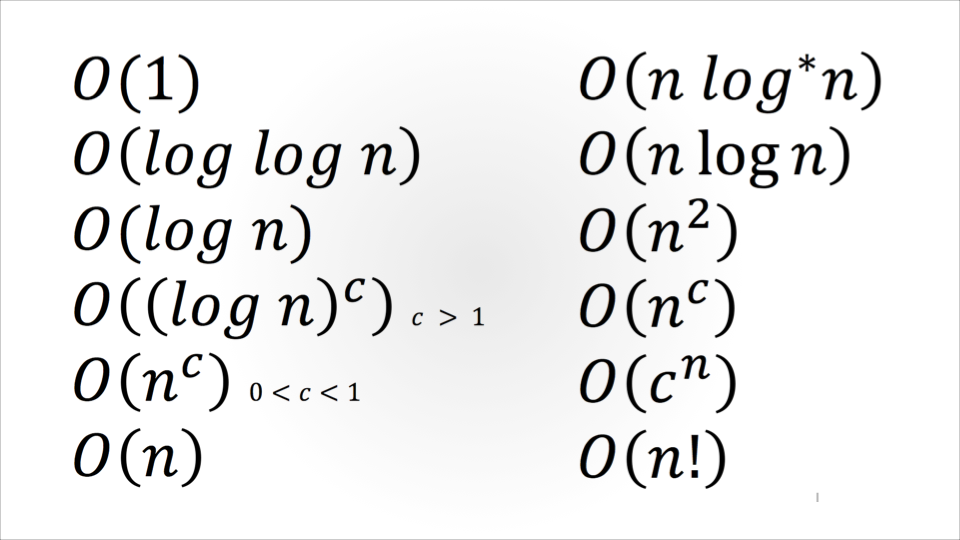
Este análisis es de vital importancia cuando como desarrolladores estamos trabajando con algoritmos que requieren de una entrada sustancial de datos, o cuando estamos trabajando con un dispositivo a bajo nivel en donde la memoria es limitada, o en aplicaciones cuya eficiencia es crítica como en sistemas de tiempo real. Y tal vez podría parecerte no tan necesario si te dedicas a programar aplicaciones para un usuario final, sin embargo es una buena idea que conozcas esta notación para que puedas elegir qué librerías, frameworks y algoritmos usarás en tus desarrollos para entregar la mejor experiencia a los usuarios.
Para esto, puedes tener en cuenta que algunas librerías y frameworks exponen la complejidad de sus operaciones, como las de .NET

Y la de Java

Existen otros tipos de notaciones que también nos ayudan a describir el comportamiento como la Pequeña O, Omega o Theta pero que no son tan usadas, al menos en ambientes no académicos.