Recursión e iteración
Seguramente si ya tienen nociones de programación ya habrán escuchado hablar de estos técnicas, pero si no, aquí te cuento sobre ellos: Comenzaré por decir que son técnicas de programación permiten solucionar problemas iguales pero viéndolos desde enfoques distintos.
Iteración
Nosotros vamos a ver a la iteración como la repetición de un conjunto de pasos con la intención de llegar a una meta. La iteración nos ayuda para cuando vamos a resolver un problema comenzando por alguna de sus partes (usualmente la más simple) para construir la solución completa.
El factorial de n o n factorial se define en principio como el producto de todos los números enteros positivos desde 1 (es decir, los números naturales) hasta n.
Piensa en el cálculo del factorial: una solución iterativa comienza con el primer valor del factorial que es el factorial de 0, que es uno:
long Factorial(int n)
{
long fact = 1;
return fact;
}
Después se itera mediante un ciclo for de 1 hasta n multiplicando el factorial realizando la operación:
long Factorial(int n)
{
long fact = 1;
for(int i = 1; i <= n; i++)
fact = fact * i;
return fact;
}
En un algoritmo iterativo se comienza por un caso base y a partir de él se construye la solución tomando en cuenta los valores que ya existen y que ya calculamos.
Si hablamos sobre el análisis de un algoritmo iterativo, veremos que no se trata mas que de ciclos que pueden ser fácilmente analizados.
Recursión
Ahora, hablemos sobre la recursión: la recursión, al igual que la iteratividad nos ayudará a resolver un problema grande mediante la repetición de una serie de pasos, con la diferencia de que en este caso, la solución del problema está definida en términos de si misma.
Comienza a atacar un problema tomando un problema grande y lo va dividiendo hasta llegar a problemas más pequeños que son sencillos o triviales de resolver. Una vez que llega a estos problemas más pequeños, vuelve por donde llegó y comienza a combinar las soluciones entre si para obtener la solución al problema más grande.
Piensa nuevamente en el cálculo del factorial, desde su definición se entiende por qué puede ser modelado como un problema recursivo:
n! = 1 si n = 0 n! = n ✖ (n-1)! si n > 0
Esta definición cumple con el par de principios de una función recursiva:
- Tienen al menos una condición de corte o terminación, y
- Está definida en términos de si misma.
Partiendo de aquí se puede crear una función recursiva:
long Factorial(int n)
{
if(n == 0)
return 1;
return n * Factorial(n - 1);
}
En este caso la función factorial está definida en términos de si misma, ya que se va llamando con un problema más pequeño a cada ocasión hasta que n vale 0 y deja de llamarse a si misma para comenzar a regresar por donde vino combinando los resultados.
En términos de eficacia las dos soluciones nos resultan útiles puesto que ambas nos llevan al resultado, sin embargo en eficiencia puede ser que no:
Modelar un problema más complicado utilizando un algoritmo iterativo es algo que podría costarnos en tiempo de diseño ya que debemos encontrar la manera ideal de almacenar el estado (o los valores previamente procesados) nosotros mismos. Usualmente se usan pilas para el almacenamiento.
Mientras que modelar un problema complicado empleando un algoritmo recursivo podrá ser sencillo para diseñar ya que el estado es preservado automáticamente cada vez que se llama a una nueva función, pero costará más tiempo al ejecutarse debido a las llamadas a funciones que ocurren constantemente.
Cualquier algoritmo iterativo puede ser transformado en recursivo y viceversa, en algunos casos la transformación es sencilla mientras que en otros es más complicada.
En términos generales cuando se prefiere una solución recursiva es solo por su cercanía con un modelo en la vida real, lo cual lo hace más sencillo de entender y reproducir.
Algoritmos como el cálculo del Fibonacci, el Factorial, la obtención del máximo común divisor son problemas triviales que son sencillos de resolver (y entender) usando iteraciones. Mientras que el cálculo de la altura de un árbol binario, el conteo de elementos en una lista o la búsqueda en grafos son problemas más entendibles definidos como recursiones.
Ahora, realizar el análisis de un algoritmo recursivo es también más complicado, y es que es básicamente resolver la relación de recurrencia que la define. Esta relación de recurrencia se obtiene de analizar el comportamiento de la función, para el factorial recursivo es:
De nueva cuenta, se divide en el caso general y los casos base, en donde cada uno tiene una complejidad asociada;
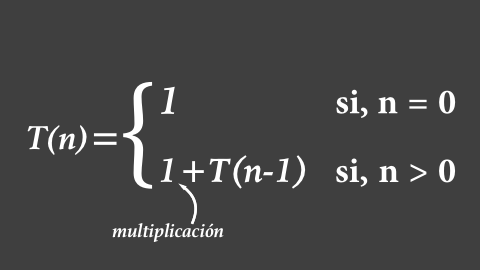
Lo cual es un tema que requiere de más explicación y probablemente de un pizarrón. En el futuro espero hacer un par de videos hablando de esto, pero si no pueden aguantar la tentación, aquí hay un par de vídeos donde se explica cómo resolver esta clase de problemas: Diseño y Análisis de Algoritmos. Recurrencias no homogéneas y Complejidad Asintótica y Ecuaciones de Recurrencia - Solución de Ecuaciones Lineales.